论文名称：

General fractal topography: an open mathematical framework to characterize and model mono-scale-invariances.

论文摘要：

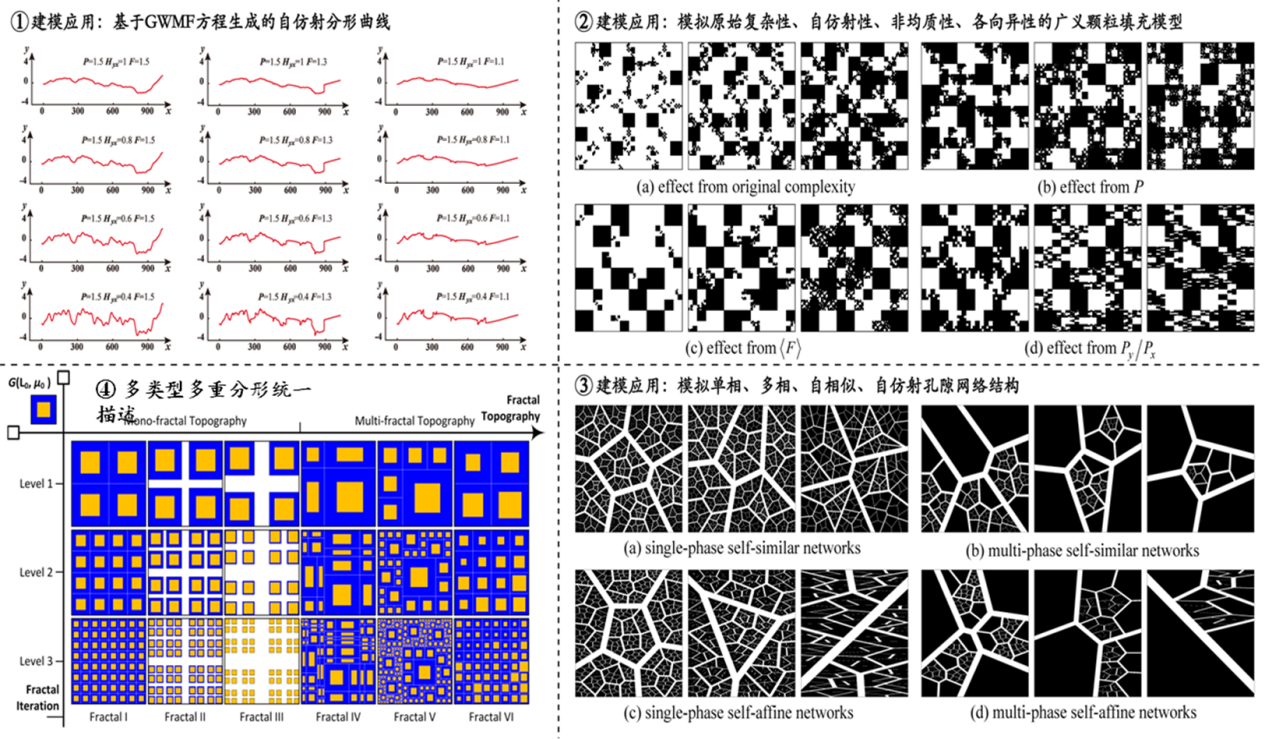
In this work, we reported there are two kinds of independent complexities in mono-scale-invariance, namely to be behavioral complexity deter-mined by fractal behavior and original one wrapped in scaling object. Quantitative characterization of the complexities is fundamentally important for mechanism exploration and essential understanding of nonlinear systems. Recently, a new concept of fractal topography (W) was emerged to define the fractal behavior in self-similarities by scaling lacunarity (P) and scaling coverage (F) as W (P, F). It is, however, a “special fractal topography” because fractals are rarely deterministic and always appear stochastic, heterogeneous, and even anisotropic. For that, we reviewed a novel concept of “general fractal topography”, W (P, F). In W, P is generalized to a set accounting for direction dependent scaling behaviors of the scaling object G, while F is extended to consider stochastic and heterogeneous effects. And then, we decomposed G into G (G₊, G₋) to ease type controlling and measurement quantification, with G₊ wrapping the original complexity while G₋ enclosing behavioral complexity. Together with W and G, a mathematical model F_3S (W , G) was then established to unify the definition of deterministic or statistical, self-similar or self-affine, single- or multi-phase properties. For demonstration, algorithms are developed to model natural scale-invariances. Our investigations indicated that the general fractal topography is an open mathematic framework which can admit most complex scaling objects and fractal behaviors.

论文亮点

①General fractal topography was established to characterize fractal behavior accounting for direction-dependent scaling behaviors and stochastic and heterogeneous distribution.

②An open mathematical framework was proposed To eases Fractal modeling And measurement quantification, which admits arbitrary scaling object and Fractal behavior.

论文出处

杂志: Nonlinear Dynamics

DOI: 10.1007/s11071-019-04931-9

主要作者

Yi Jin* , Xianhe Liu , Huibo Song ,et al.